지난 포스팅에서는 NumPy를 활용해서 간단하게 벡터 연산과 행렬 연산을 해보았다. 이번 포스팅에서 다룰 내용은 기초라고는 할 수 없지만 앞으로 NumPy를 활용해서 다른 모양의 배열 간의 연산을 수행할 때 꼭 이해해야 하는 개념인 브로드캐스팅을 알아야 하기 때문에 이를 소개하고자 한다.
2017/10/09 - [Data Science/Python] - Python 기초 - NumPy로 선형대수 표현하기 (1)
선형대수 Linear Algebra
3. 브로드캐스팅 Broadcasting
3. 브로드캐스팅 Broadcasting
브로드캐스팅이라고 하면 우리는 "방송"이라는 단어가 생각나 브로드캐스팅이 왜 파이썬에서 나온거냐고 그 개념이 잘 와닿지 않을 수 있다. Dictionary.com에서 broadcast로 검색을 해봤더니
He broadcast his punch and the other man was able to parry it.
위와 같은 결과가 나왔다. 1번과 2번은 우리가 잘아는 방송과 관련된 뜻이었지만, 그 밑을 보면 broadcast란 단어는 무언가를 '흩뿌리고 퍼뜨리고 전파'할 때 사용하는 것이라는 것을 알 수 있다. 아래 그림을 보면서 전파한다는 의미를 더 설명해보도록 하겠다.
일반적으로 NumPy에서 모양이 다른 배열끼리는 연산이 불가능하다.
In [167]: a = np.array([1,2,3])
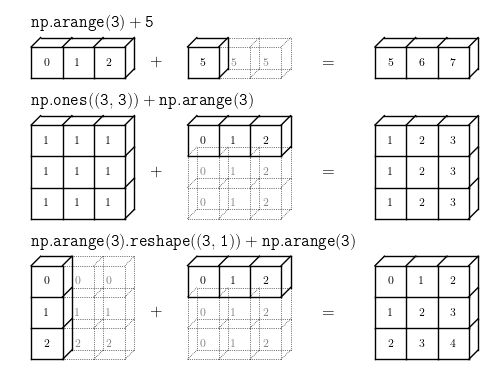
- 차원의 크기가 1일때 가능하다
두 배열 간의 연산에서 최소한 하나의 배열의 차원이 1이라면(0번 축이든 1번 축이든; 1행이든 1열이든) 가능하다. - 차원의 짝이 맞을 때 가능하다
차원에 대해 축의 길이가 동일하면 브로드캐스팅이 가능하다.
두 번째 그림은 3x3 인 배열과 1x3인 배열의 연산이다. 2번 조건을 만족하여 브로드캐스팅이 수행되었다. 1x3 배열이 브로드캐스팅되어 3x3 배열로 변형되어 연산이 수행되었다.
세 번째 그림은 3x1 인 배열과 1x3인 배열의 연산이다. 1번 조건을 만족하여 브로드캐스팅이 수행되었다. 3x1인 배열은 길이가 1인 차원에 대해 반복 확장되었고, 1x3인 배열도 마찬가지로 길이가 1인 차원에 대해 반복 확장되었고 확장된 두 배열 간에 연산이 일어났다.
아래는 3차원 배열의 0번 축으로 브로드캐스팅 된 예시이다. 만족스러운 그림이 없어서 직접 만들어보았다. 3,4,2의 길이를 가진 3차원 배열과 4,2의 길이를 가진 2차원 배열이 있다. 위에서 말한 조건처럼 차원의 짝이 맞아야 브로드캐스팅이 수행될 수 있다. 2차원 배열의 4,2가 3차원 배열의 4,2와 짝이 맞기 때문에 누락된 부분인 3만큼의 차원 확장(broadcasting)이 되고 합 연산이 수행된다. 0번 축으로 브로드캐스팅이 되었다.
브로드캐스팅은 저차원의 배열을 연산을 위해서 고차원 배열로 확장시키는 것과 같다.
위의 그림을 NumPy로 브로드캐스팅을 통해 쉽게 연산이 된다. 아래는 위의 그림을 코드로 돌려본 결과이다.
In [171]: array3d = np.array([[[0,1], [2,3], [4,5], [6,7]],
...: [[8,9], [10,11],[12,13],[14,15]],
...: [[16,17],[18,19],[20,21],[22,23]]])
...:
In [172]: array3d
Out[172]:
array([[[ 0, 1],
[ 2, 3],
[ 4, 5],
[ 6, 7]],
[[ 8, 9],
[10, 11],
[12, 13],
[14, 15]],
[[16, 17],
[18, 19],
[20, 21],
[22, 23]]])
In [173]: array2d = np.array([[0,1],[2,3],[4,5],[6,7]])
In [174]: array2d
Out[174]:
array([[0, 1],
[2, 3],
[4, 5],
[6, 7]])
In [175]: array3d + array2d
Out[175]:
array([[[ 0, 2],
[ 4, 6],
[ 8, 10],
[12, 14]],
[[ 8, 10],
[12, 14],
[16, 18],
[20, 22]],
[[16, 18],
[20, 22],
[24, 26],
[28, 30]]])
아래는 array를 차원에 따라 어떤 모양을 하고 있는지 그리고 축(axis)은 어떻게 구성되었는지 참고할 만한 그림이다.

출처: https://www.safaribooksonline.com/library/view/elegant-scipy/9781491922927/ch01.html
참고자료
1. 웨스 맥키니. 파이썬 라이브러리를 활용한 데이터분석. 한빛미디어. 2013
2. https://kakalabblog.wordpress.com/2017/04/03/zen-of-numpy/
'Data Science > 파이썬으로 데이터분석 하기' 카테고리의 다른 글
| 파이썬으로 데이터 분석하자 (5) - Matplotlib 기본 (2) | 2017.12.08 |
|---|---|
| 파이썬으로 데이터분석하자 (4) - Pandas 기본 (7) | 2017.12.06 |
| 파이썬으로 데이터 분석하자 (3) - NumPy 기본 (4) | 2017.10.09 |
| Python 기초 - NumPy로 선형대수 표현하기 (1) (2) | 2017.10.09 |
| 파이썬으로 데이터 분석하자 (2) - IPython 사용하기 (1) | 2017.09.27 |
| Python 기초 - 일급함수(first-class)란 무엇인가 (2) | 2017.09.20 |
| 파이썬으로 데이터 분석하자 (1) (1) | 2017.09.19 |

댓글