문과생도 이해하는 딥러닝 (5) - 신경망 학습 실습
2017/09/27 - 문과생도 이해하는 딥러닝 (1) - 퍼셉트론 Perceptron
2017/10/18 - 문과생도 이해하는 딥러닝 (2) - 신경망 Neural Network
2017/10/25 - 문과생도 이해하는 딥러닝 (3) - 오차 역전파, 경사하강법
2017/12/24 - 문과생도 이해하는 딥러닝 (4) - 신경망구현, 활성화함수, 배치
신경망 알고리즘으로 모델을 만들고 학습하는 방법에 대해 간단하게 실습을 진행하였다. 그리고 학습할 때 필요한 필수 개념인 손실함수, 배치, 기울기, 학습률에 대해서 알아보았다. 수학적 개념만으로는 이해하기 어려운 부분들이 다소 있었으나 코드를 보면서 진행하니 확실히 각 개념과 역할에 대해서 이해하기 수월하였다.
신경망 학습 Learning 실습
문과생도 이해하는 딥러닝 (5)
- 데이터를 탐색한 후 전처리하고
- 데이터 변수 등을 분석하여 전체 훈련용, 테스트용 데이터 셋을 구성한 다음
- 해결하고자 하는 문제에 맞는 알고리즘을 선택하여 모델을 만든 후
- 훈련용 데이터 셋으로 모델을 학습시키고
- k-folds 교차검증 및 테스트용 데이터 셋 으로 모델 간 검증을 진행하고
- 최고의 성능을 보이는 모델을 최종 배치한다.
1. 손실 함수 Loss Function
1) 평균제곱오차 Mean Squared Error
def mean_squared_error(y, t):
return 0.5*np.sum((y-t)**2)
#정답은 2
t = [0,0,1,0,0,0,0,0,0,0]
y1 = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
print(mean_squared_error(np.array(y1), np.array(t)))
y2 = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
print(mean_squared_error(np.array(y2), np.array(t)))
2) 교차 엔트로피 오차 Cross Entropy Error
def cross_entropy_error(y,t):
delta = 1e-7
return -np.sum(t * np.log(y+delta))
y + delta인 이유는 만약 y가 0일 때는 infinite 값을 반환하므로 계산이 안되기 때문에 아주 작은 임의의 값을 입력하여 값이 -inf가 되는 것을 막는다
t = [0,0,1,0,0,0,0,0,0,0]
y1 = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
print(cross_entropy_error(np.array(y1), np.array(t)))
y2 = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
print(cross_entropy_error(np.array(y2), np.array(t)))
평균제곱오차에서 계산한 것과 동일하게 처음의 예측이 더 잘맞았음을 교차엔트로피 오차로 확인할 수 있다.
2. 미니배치 학습 Mini-Batch
from mnist import load_mnist
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
print(x_train.shape)
print(t_train.shape)
train_size = x_train.shape[0]
batch_size = 10
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
np.random.choice(train_size, batch_size)
10개에 대한 인덱스가 무작위로 추출된 모습이다
# 타겟이 one-hot encoding 방식일 경우
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(t*np.log(y))/batch_size
# 타겟이 단순 레이블 형태일 경우
def cross_entropy_error(y,t):
if y.ndim == 1:
t = t.reshpae(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size),t]))/batch_size
3. 미분

1) 수치미분
# 중심차분, 중앙차분
def numercial_diff(f, x):
h = 1e-4
return (f(x+h)-f(x-h))/2*h
def function_1(x):
return 0.01*x**2 + 0.1*x
x = np.arange(0.0, 20.0, 0.1)
y = function_1(x)
plt.xlabel("x")
plt.ylabel("f(x)")
plt.plot(x,y)
plt.show()
# x = 5 일 때, 함수의 미분 계산
print(numercial_diff(function_1, 5))
# x = 10 일 때, 함수의 미분 계산
print(numercial_diff(function_1, 10))
이렇게 계산한 미분 값이 x에 대한 f(x)의 변화량이다. 함수의 기울기를 의미한다. 해석학적으로 이를 풀이해도 0.2와 0.3으로 오차가 매우 작음을 알 수 있다. 거의 같은 값이다.
2) 편미분
def function_2(x):
return x[0]**2 + x[1]**2
# x0 = 3, x1 = 4 일 때, x0에 대한 편미분
def function_tmp1(x0):
return x0*x0 + 4.0**2.0
print(numercial_diff(function_tmp1, 3.0))
# x0 = 3, x1 = 4 일 때, x1에 대한 편미분
def function_tmp2(x1):
return 3.0**2.0 + x1*x1
print(numercial_diff(function_tmp2, 4.0))
4. 기울기 Gradient
1) 경사하강법
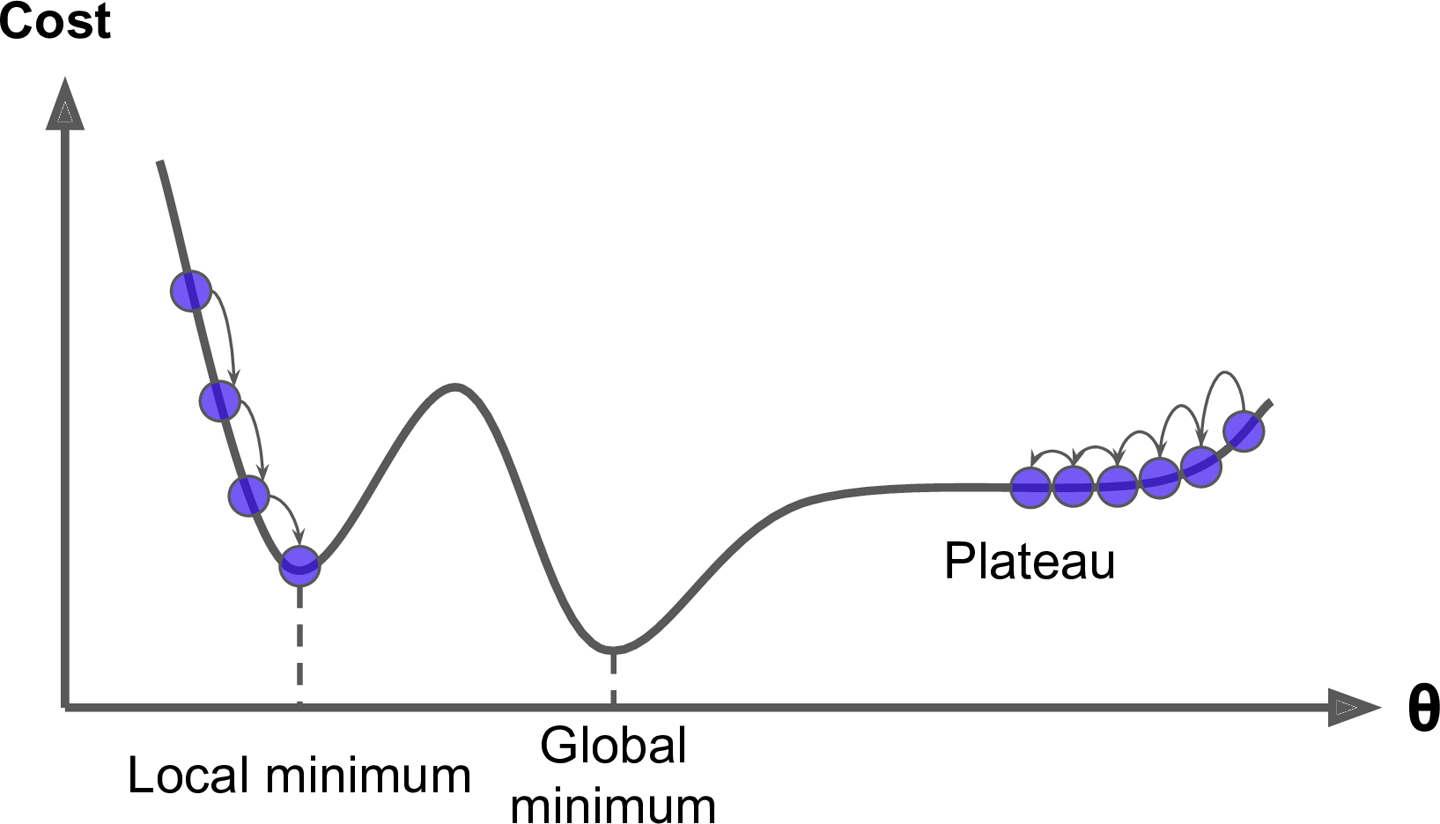
def numerical_gradient(f, x):
h = 1e-4
grad = np.zeros_like(x)
for idx in range(x.size):
tmp_val = x[idx]
#f(x+h) 계산
x[idx] = tmp_val + h
fxh1 = f(x)
#f(x-h) 계산
x[idx] = tmp_val - h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val
return grad
# 임의의 세 점에서의 기울기 계산 (수치미분)
print(numerical_gradient(function_2, np.array([3.0, 4.0])))
print(numerical_gradient(function_2, np.array([0.0, 2.0])))
print(numerical_gradient(function_2, np.array([3.0, 0.0])))
Learning Rate
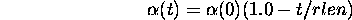
def gradient_descent(f, init_x, lr= 0.01, step_num=100):
'''
f는 최적화려는 함수
init_x는 초깃값
lr은 학습률
step_num은 경사법에 따른 반복 횟수
함수의 기울기는 앞서 정의한 numerical_gradient로 구하고
그 기울기에 학습률을 곱한 값으로 갱신하는 처리를 setp_num번 반복
'''
x = init_x
for i in range(step_num):
grad = numerical_gradient(f, x)
x -= lr * grad
return x
학습률이 너무 크거나 작으면 좋은 결과를 얻기가 힘들다
# 학습률이 너무 큰 경우 lr = 10.0
init_x = np.array([-3.0, 4.0])
gradient_descent(function_2, init_x=init_x, lr=10.0, step_num=100)
# 학습률이 너무 작은 경우 lr = 1e-10
init_x = np.array([-3.0, 4.0])
gradient_descent(function_2, init_x=init_x, lr=1e-10, step_num=100)
2) 신경망에서의 기울기
from scratch.common.functions import softmax, cross_entropy_error
from scratch.common.gradient import numerical_gradient
class simpleNet:
def __init__(self):
self.W = np.random.randn(2,3)
def predict(self, x):
return np.dot(x, self.W)
def loss(self,x, t):
z = self.predict(x)
y = softmax(z)
loss = cross_entropy_error(y, t)
return loss
net = simpleNet()
print(net.W)
x = np.array([0.6, 0.9])
p = net.predict(x)
print(p)
np.argmax(p)
t = np.array([0,0,1])
net.loss(x, t)
def f(W):
return net.loss(x, t)
dW = numerical_gradient(f, net.W)
print(dW)
5. 학습 알고리즘 구현
1) 전제
2) 1단계: 미니배치
3) 2단계: 기울기 산출
4) 3단계: 매개변수 갱신
5) 1~3 단계 반복
학습 횟수가 늘어날수록 손실 함수의 값이 떨어진다면 이는 신경망의 가중치들이 학습 데이터에 잘 맞아들고 있음을 의미하며 이를 학습이 잘되고 있다고 볼 수 있다.
신경망 모델 클래스 생성
from scratch.common.functions import *
from scratch.common.gradient import numerical_gradient
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
def predict(self, x):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
return y
def loss(self, x, t):
y = self.predict(x)
return cross_entropy_error(y, t)
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis = 1)
t = np.argmax(t, axis = 1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads
net = TwoLayerNet(input_size=784, hidden_size=100, output_size=10)
net.params['W1'].shape # (784, 100)
net.params['b1'].shape # (100,)
net.params['W2'].shape # (100, 10)
net.params['b2'].shape # (10,)
예제로 2층 신경망 학습시켜보기
nuemrical_gradient는 수치미분으로 기울기를 계산하기 때문에 계산이 오래 걸린다. 신경망이 그렇게 복잡하지 않음에도 상당한 시간이 소요됐다.
x = np.random.rand(100, 784)
t = np.random.rand(100, 10)
%time grads = net.numerical_gradient(x, t)
print(grads['W1'].shape)
print(grads['b1'].shape)
print(grads['W2'].shape)
print(grads['b2'].shape)
검증 testing
하지만 오버피팅의 문제가 있을 수 있으므로 이를 확인하기 위해서 테스트 데이터를 통해서 일반적으로 잘 들어맞는지 확인할 필요가 있다. 오버피팅overfitting은 학습한 모델이 학습 데이터에만 잘들어 맞고 다른 실제 상황에서 잘 맞지 않음을 말한다.
이를 위해서 하나의 epoch 단위 별로 훈련 데이터와 테스트 데이터에 대한 모델의 정확도를 확인할 필요가 있다.
Epoch 에포
- iter_num : 가중치 갱신을 몇 번 하는지
- train_size : train 데이터의 총 개수
- batch_size : 한 번에 학습을 다하기 어려우니 나누어서 갱신을 하는데 이때 미니배치를 사용하며 배치 사이즈는 몇 개씩 뽑아서 쓸 것인지... 한 번의 기울기 갱신에 몇 개의 train 데이터를 사용할 것인지 그 개수를 의미
- epoch : 하나의 단위로 train_size/batch_size로 구하며 하나의 미니배치에 대해서 갱신을 몇 번 해야 전체 train 데이터에 대해서 한 번의 학습이 가능한지를 나타낸다. 100개의 train_size에 batch_size가 10이면 10번의 iter로 한 번의 학습이 가능하므로 epoch는 10이 된다. 10번 미니배치를 추출해서 기울기 계산과 가중치를 업데이트하면 한 번 전체 train 데이터에 대해서 학습했다고 볼 수 있다.
- # of epochs : 총 iter(기울기 계산, 가중치 업데이트) 횟수를 epoch의 단위로 나누면 전체 train 데이터에 대해서 몇 번 학습했는지 알 수 있다. 예를 들어 10,000개의 데이터에 대해서 가중지 업데이트를 1,000번 한다고 했을 때, 배치 사이즈를 1,000이라고 한다면 epoch 단위는 10이 된다. 따라서 # of epochs는 100번(= 1,000/10)이 된다. 학습은 총 10번 하게 되는 것이다.
예제로 미니배치와 에포를 이용해서 학습을 한 결과는 학습이 끝나고 업로드하겠다.
생각보다 계산량이 많아서 기울기 계산과 가중치 업데이트에 시간이 오래걸린다.
기본적인 신경망이 학습이 정말 오래 걸린다는 것을 깨달았다. 이러한 문제를 해결하기 위해서 오차역전파 방법이 빠르게 기울기를 계산할 수 있도록 한다고 하니 다음 포스팅에서 이를 다루도록 하겠다.