NTN으로 시작하는 자연어처리와 딥러닝 (4) - 모델 학습
『NTN으로 시작하는 자연어처리와 딥러닝』
지난 포스트에서는 NTN 모델이 신경망 아키텍처는 어떻게 생겼고, 그것을 구성하는 layer에 대해서 알아보았습니다. 이번에는 구축한 아키텍처와 layer를 어떻게 학습시키는지 머신러닝 프로세스를 중심으로 중요 학습 Techniques와 함께 알아보도록 하겠습니다.
*핵심 개념에 대한 사전을 이전 포스트에 정의하였으니 먼저 보시는 것을 추천드립니다.
NTN은 Neural Tensor Network의 약자로 스탠포드 대학교 교수인 Richard Socher (2013)가 "Reasoning With Neural Tensor Networks for Knowledge Base Completion"에서 지식을 넘어선 추론(Reasoning Over Knowledge)을 위해 제시한 딥러닝 모델입니다.
모델 학습은 어떻게?
Neural Models for Reasoning over Relations
딥러닝도 기계학습의 한 부분으로 전체적인 맥락에서의 학습 프로세스는 일반적인 기계학습의 그것과 비슷합니다. 여기에서는 스탠포드 교수인 앤드류 응(Andrew Ng.)이 설명한 Neural Network 학습 프로세스에 기초해서 NTN을 설명하도록 하겠습니다. NTN은 앞에서 설명하였듯이 Single Layer 기반의 신경망 모델입니다.
< Andrew Ng.'s Neural Network Learning Process >
1. pick NN architecture 신경망 아키텍처 설정
2. choose layout NN (# of hidden units, how many layers) 신경망 모델의 unit, layer 등을 설정
3. Training NN 신경망 학습
- weight initialization 가중치 초기화
- implement forward propagation 순전파
- implement cost function 손실함수 계산
- implement backpropagation to compute partial derivatives 오차역전파 및 기울기 편미분 계산
- gradient checking to confirm BP
- gradient descent or Optimization function to minimize cost function with the weights in theta 손실함수 최소화를 위한 최적화
들어가기에 앞서, 이번 포스트에서 다루는 파트가 하나의 프로젝트 관점으로 봤을 때 학습 프로세스가 위치하는 단계가 어디쯤인지 보자면, 먼저 일반적인 신경망 모델 구축의 전체적인 과정은 다음과 같습니다.
< 일반적인 신경망 모델 구축 순서 >
1. 문제 정의
2. 데이터 준비
3. 데이터셋 생성
4. 모델 구성
5. 모델 학습과정 설정
6. 모델 학습
7. 모델 평가
8. 모델 사용
이번 포스트에서 다루는 부분은 '모델 학습과정 설정'과 '모델 학습'입니다. 이전 포스트에서는 아키텍처를 다루었고 이는 4번 '모델 구성'에 해당 합니다. 모델을 학습하기 위해서는 모델을 어떻게 학습할 것인지 다양한 파라미터들을 설정하고 조정해야 합니다.
1. Pick Neural Network Architecture
NN 아키텍처는 아래 형식입니다. 개별의 작은 하얀색 박스 (Rn)은 앞에서 정의한 Neural Tensor Layer입니다. 따라서 하나의 R은 하나의 모델이라고도 볼 수 있습니다.
NTN은 각 모델 별로 각각의 개별 relation에 대해서 그 관계를 분석합니다.(link prediction) 전체로 크게 봤을 때는 layer의 층이 깊지는 않으나 수 많은 신경(Perceptron)으로 구성된 신경망 모형이라고 볼 수 있습니다. 최종적으로는 모든 relation의 신경망 모델을 통합하여 사용하기 때문입니다.
이것이 의미하는 바는 각 relation의 신경망 모델 마다 고유하게 모델을 구성하고 학습 파라미터들을 갖게 된다는 것입니다. 설정된 모델 학습과정이 동일하다고 할 지라도 모델마다 파라미터의 값은 달라지게 됩니다.
2. Choose Layout Neural Network
3. Training Neural Network (모델 학습과정 설정 및 학습)
(1) Weight Initialization 가중치 초기화
sqrt(6 / (fan_in + fan_out))
와 같은 방식이며 fan_in은 weight tensor input unit개수를, fan_out은 weight tensor output unit의 개수를 의미합니다.
자세한 내용은 Understanding the difficulty of training deep feedfoward neural networks에서 확인하시면 좋습니다. tensorflow와 keras에서 이를 초기화 방법을 지원하고 있는 것으로 보입니다. Glorot, Bengio(2010)의 실험결과에 따르면 hyper tangengt 함수를 위해서는 standard보다는 normalized 방식을 사용하는 것이 weight의 분포와 갱신을 위해서 더 나은 성능을 보인다고 합니다.
Weight initialization의 분포는 다음과 같습니다. W ~ U [ -root(6/(n+n)), root(6/(n+n)) ]
NTN의 저자 Socher 교수 역시 최근 자신의 강의에서 tanh에 대해 Glorot uniform initialization을 하는 것이 가장 좋다고 소개하기도 하였습니다.
(2) Feed Forward Propagation 순전파
순전파는 W'X + b의 형태로 순차적으로 계산한 값을 전파하는 방법입니다. 앞의 포스트에서 다루었기 때문에 여기서 더 다루지는 않도록 하겠습니다.
NTN에서는 score funciton을 계산하는 것이라고 생각하면 됩니다. 가중치 초기화를 통해서 u, W, V, b, E에 대한 가중치 weight가 생성되고 일단 순전파를 통해서 score를 계산합니다.
(3) Cost Function 손실함수
손실 함수에서 손실(cost 또는 loss)이 의미하는 것은 일종의 error, 즉 오차를 의미합니다. 위에서 weight parameter들로 순전파를 통해 나온 값이 실제값과 비교했을 때 얼마만큼 오류가 있었는지 측정하는 하나의 지표로 손실함수가 사용됩니다.
따라서 설정한 모델은 이 손실함수의 값을 최소화하는 방향으로 학습을 진행하게 됩니다. 즉, 오차가 적은 모델을 만들어나가는 것입니다. NTN에서도 오차를 측정하기 위한 손실함수가 있습니다.
손실함수의 다른 이름인 목적 함수(Objective Function)로 이를 설명합니다.
NTN의 손실함수는 contrastive max-margin objective function이라는 이름으로 소개됩니다. 이 목적함수의 주요 아이디어는 각 정답 triplet (e1, R, e2)의 score가 무작위로 만들어낸 triplet보다 항상 높은 score를 받도록 하자는 것입니다.
다시 말하면, 랜덤하게 triplet을 만들어서 이것은 일종의 False dataset과 비교해서 True dataset에 높은 점수를 줘서 True Dataset에 맞도록 가중치들을 학습하자는 의미입니다.
그런데 이 손실함수는 구글링을 해도 나오지 않을 것입니다. 왜냐하면 Socher 자신이 여러 개념들을 섞어서 만든 Customized 손실함수이기 때문입니다.
NTN의 손실함수는 크게 2가지의 개념을 내포하고 있습니다.
하나는 Hinge Loss.... 다른 하나는 Negative Sampling 입니다.
간단하게 말하면 Hinge Loss는 SVM을 공부할 때 나오는 max-margin을 구하는 loss function이고, Negative sampling은 NLP에서 Skip-gram 방식을 사용하는 것인데 정답 데이터 세트만 있을 때 임의적으로 오답 셋을 만들어 오차를 구하는 방식입니다.
NTN의 Contrastive Max-margin Objective Function은 다음과 같습니다.
손실함수 J(Ω)를 최소화하는 것이 학습의 목적입니다. 그래서 목적 함수라고도 부릅니다.
Hinge Loss
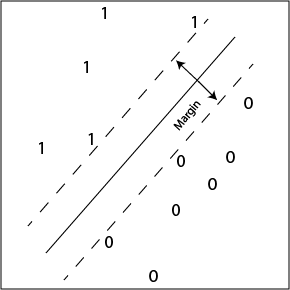
Max-margin 키워드에 해당하는 내용입니다. Support Vector Machine의 알고리즘과 손실함수를 알고계신 분들이라면 익히 알고 계신 내용입니다. SVM 선형 분류 시에 margin을 최대화하는 방식으로 decision boundary를 설정할 때 주로 사용합니다. SVM 선형분류는 이진 분류의 개념과 가깝습니다.
우리가 해결하고자 하는 문제는 간단하게 접근하면 triplet (e1, R, e2)가 참이냐고 묻는 것이기 때문에, 0또는 1을 결과로 나오는 이진분류(binary classification)를 의미합니다. 이진분류를 위한 많은 오차 계산 방식이 있지만 (cross-entropy 등) hinge loss를 사용한 것으로 보입니다.
참고: Chris Thornton [link]
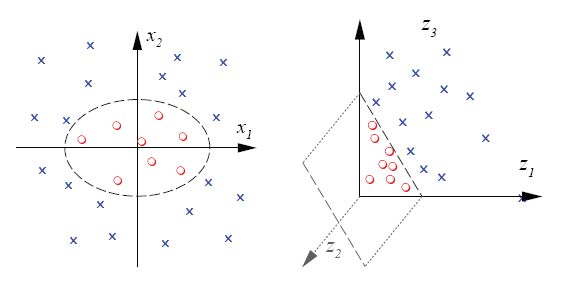
위와 같이 Weight Vector Space 공간에서 정답과 오답을 분류를 해주는 초평면(hyperplane)을 만들기 위해서 Hinge Loss를 사용한 것입니다.

출처: ratsgo's blog

