2017/09/27 - 문과생도 이해하는 딥러닝 (1) - 퍼셉트론 Perceptron
2017/10/18 - 문과생도 이해하는 딥러닝 (2) - 신경망 Neural Network
2017/10/25 - 문과생도 이해하는 딥러닝 (3) - 오차 역전파, 경사하강법
2017/12/24 - 문과생도 이해하는 딥러닝 (4) - 신경망구현, 활성화함수, 배치
2017/12/26 - 문과생도 이해하는 딥러닝 (5) - 신경망 학습 실습
2018/01/05 - 문과생도 이해하는 딥러닝 (6) - 오차역전파법 실습 1
2018/01/05 - 문과생도 이해하는 딥러닝 (7) - 오차역전파법 실습 2
2018/01/07 - 문과생도 이해하는 딥러닝 (8) - 신경망 학습 최적화
2018/01/07 - 문과생도 이해하는 딥러닝 (9) - 신경망 초기 가중치 설정
2018/01/07 - 문과생도 이해하는 딥러닝 (10) - 배치 정규화
이전 포스팅에서 다룬 배치 정규화는 일종의 정규화(Regularization) 기법이라고 볼 수 있다. 과적합(overfitting)의 위험을 줄이고 학습속도를 개선하는 등의 문제를 해결하기 위해 고안된 것이다. 배치 정규화 이외에도 가중치 감소(Weight Decay), 드롭아웃(Dropout) 등이 비슷한 목적을 위해서 제안된 방법들이다.
머신러닝에서는 학습된 모델이 학습 데이터에만 높은 정확도를 보이길 원치 않는다. 궁극적으로 학습한 모델이 범용적으로 사용되어야 하기 때문에 학습 데이터에만 잘맞는 overfitting 문제를 피해야 한다. 신경망의 층이 깊어질수록, 학습률이 작을수록 과적합되는 경향이 있다.
가중치 감소, 드롭아웃
문과생도 이해하는 딥러닝 (11)
1. 가중치 감소 Weight Decay
가중치 감소는 학습 중에 가중치가 큰 것에 대해서는 일종의 패널티를 부과해 과적합의 위험을 줄이는 방법이다. 가중치의 제곱 법칙(L2 법칙; 많이 사용된다)를 손실함수에 더해 손실함수 값이 더 커지게 한다. 그만큼 가중치가 커지는 것을 억제하기 되는 것이다.
L2 법칙은 1/2곱하기 λ(람다) 곱하기 W제곱 이다.
람다는 정규화의 세기를 조절하는 하이퍼파라미터이다.
람다를 크게 설정할수록 가중치에 대한 페널티가 커진다.
가중치 감소 이전 (Overfitting)
가중치 감소 이후
2. 드롭아웃 Dropout
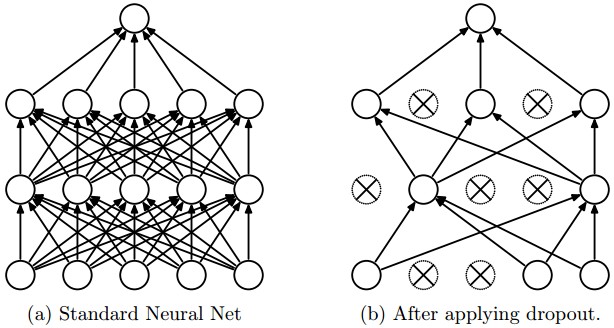
드롭아웃 적용 전
드롭아웃 적용 후
class Dropout:
def __init__(self, dropout_ratio=0.5):
self.dropout_ratio = dropout_ratio
self.mask = None
def forward(self, x, train_flg=True):
if train_flg:
self.mask = np.random.rand(*x.shape) > self.dropout_ratio
return x * self.mask
else:
return x * (1.0 - self.dropout_ratio)
def backward(self,dout):
return dout * self.mask
from scratch.common.multi_layer_net_extend import MultiLayerNetExtend
from scratch.common.trainer import Trainer
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
# 오버피팅을 재현하기 위해 학습 데이터 수를 줄임
x_train = x_train[:300]
t_train = t_train[:300]
# 드롭아웃 사용 유무와 비울 설정 ========================
use_dropout = True # 드롭아웃을 쓰지 않을 때는 False
dropout_ratio = 0.2
# ====================================================
network = MultiLayerNetExtend(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100],
output_size=10, use_dropout=use_dropout, dropout_ration=dropout_ratio)
trainer = Trainer(network, x_train, t_train, x_test, t_test,
epochs=301, mini_batch_size=100,
optimizer='sgd', optimizer_param={'lr': 0.01}, verbose=True)
trainer.train()
train_acc_list, test_acc_list = trainer.train_acc_list, trainer.test_acc_list
# 그래프 그리기==========
markers = {'train': 'o', 'test': 's'}
x = np.arange(len(train_acc_list))
plt.plot(x, train_acc_list, marker='o', label='train', markevery=10)
plt.plot(x, test_acc_list, marker='s', label='test', markevery=10)
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()
드롭아웃은 머신러닝에서 자주 나오는 앙상블 기법(Ensemble)과 유사하다. 앙상블 기법은 서로 다른 모델들을 학습해서 개별 모델들에서 나온 출력의 평균을 내어 추론하는 학습 방식이다. 드롭아웃은 학습할 때 뉴런을 무작위로 학습해 매번 다른 모델들을 학습시킨다는 측면에서 앙상블 기법과 유사하다.
'Data Science > 문과생도 이해하는 딥러닝' 카테고리의 다른 글
| 문과생도 이해하는 딥러닝 (10) - 배치 정규화 (2) | 2018.01.07 |
|---|---|
| 문과생도 이해하는 딥러닝 (9) - 신경망 초기 가중치 설정 (4) | 2018.01.07 |
| 문과생도 이해하는 딥러닝 (8) - 신경망 학습 최적화 (6) | 2018.01.07 |
| 문과생도 이해하는 딥러닝 (7) - 오차역전파법 실습 2 (0) | 2018.01.05 |
| 문과생도 이해하는 딥러닝 (6) - 오차역전파법 실습 1 (0) | 2018.01.05 |
| 문과생도 이해하는 딥러닝 (5) - 신경망 학습 실습 (7) | 2017.12.26 |
| 문과생도 이해하는 딥러닝 (4) - 신경망구현, 활성화함수, 배치 (10) | 2017.12.24 |
| 문과생도 이해하는 딥러닝 (3) - 오차 역전파, 경사하강법 (2) | 2017.10.25 |
댓글